Warum? Weil Browserinkompatibilitäten in diesem Spiel mal nicht auftreten! - Reversi ist eins meiner frühen Spiele, es wurde entwickelt für und getestet mit dem IE4 und NN4.5 bis 4.7. Ein Jahr später kamen mir die Erfahrungen, die ich dabei machte, für meine Crossbrowser-Bibliothek zugute.
Reversi oder auch Othello ist ein einfaches Brettspiel, bei dem man gegnerische Steine zwischen eigenen "einfangen" muss und sie so zu eigenen umdreht. Dieses Spiel fasziniert deshalb, weil zu einer Zeit das Brett fast vollständig von einem Spieler beherrscht wird, einige Züge danach kann alles wieder komplett anders sein.
| zum Seitenanfang | ||
| zum Seitenende |
Reversi wird auf einem 8x8 großem Brett gespielt. Es gibt die Optionen Parallelstart und Diagonalstart, wobei letzterer häufiger angewendet wird. Das Spiel ist ursprünglich gedacht für 2 Spieler, die vor dem Bildschirm sitzen, alternativ soll auch gegen den Computer gespielt werden können. Der Schwierigkeitsgrad soll dabei variabel sein.
Auf dem Blatt Papier sollte man also alle Elemente einzeichnen, die man braucht, um das Spiel zu steuern. Das sind ausserdem noch ein Button für Neustart, Hilfeanzeige, Fenster schließen oder einen Link zu einer Hauptseite.
Hier fertigen wir uns als erstes eine Liste an, die für das Spiel so alles gebraucht wird, und überlegen, wie wir das dem Spiel alles einbauen. Wir brauchen:
| zum Seitenanfang | ||
| zum Seitenende |
ima0.gif, ima1.gif,
ima0_a.gif und ima1_a.gif.
leer.gif, leer0.gif,
leer1.gif).
butt.gif) und zwei Zaunspitzen (ecke.gif, ecke_a.gif)
| zum Seitenanfang | ||
| zum Seitenende |
Der Hilfebildschirm und der Endebildschirm soll ein reines Textdokument enthalten, also schreibt man eine
kurze Anleitung und speichert sie unter hilfe.htm bzw. ende.htm ab.
Hilfsdokumente und Hauptdokument sollen das gleiche Layout wie eine vorgegebene Seite haben,
das lässt sich mit einem externen Stylesheet am einfachsten bewerkstelligen.
Man kann mit CSS wunderschön gestylte Knöpfe erzeugen mit kunstvollen Rändern, aber im günstigsten Fall werden diese im NN4 nicht dargestellt, die Ränder erscheinen ganz woanders, oder der Browser verweigert die weitere Zusammenarbeit (insbesondere dann, wenn Input-Felder Rahmen bekommen sollen).
Aus diesem Grund wird mit dem oben erwähnten Hintergrundbild für die Linkleiste gearbeitet. Dazu erstellt
man sich die Klasse butt mit dem Hintergrundbild des Zaunes: .butt {
background-image:url("butt.gif"); }. Diese wird später mit class="butt"
bei Bedarf eingebunden.
Das ganze Stylesheet sieht folgendermaßen aus:
my_sytle.css
body,td,input,select
{ font-family:verdana,arial,helvetica,geneva;
font-size:10pt;
font-weight:bold;
color:#ffffcc;
background-color:#335544;
}
a:link,a:visited
{ font-family:verdana,arial,helvetica,geneva;
font-size:10pt;
font-weight:bold;
color:#335544;
text-decoration:none;
}
a:hover
{ font-family:verdana,arial,helvetica,geneva;
font-size:10pt;
font-weight:bold;
color:#990000;
text-decoration:underline;
}
a:active
{ font-family:verdana,arial,helvetica,geneva;
font-size:10pt;
font-weight:bold;
color:#ffffcc;
text-decoration:underline;
}
.butt
{ background-color:#99aa88;
background-image:url(butt.gif);
text-align:center;
}
| zum Seitenanfang | ||
| zum Seitenende |
Der Blick des Lesers fällt meist in die obere Seitenmitte des Dokumentes, also wird die Aussentabelle zentriert.
Und damit bei größeren Bildschirmen die Tabellenelemente nicht meilenweit über den Bildschirm verstreut
werden, bekommt die Tabelle eine feste Breite. Die mittlere Zelle braucht dabei Bildbreite x Zellen pro
Zeile, das sind 24x8=192 Pixel, der Beschriftung der Linkleiste gönnte ich 160 Pixel, dazu 12 für die
"Zaunspitze", also 172 Pixel. Aus ästhetischen Gründen sollte die rechte Zelle ähnlich breit
sein, wir brauchen also mindestens ca. 540 Pixel. Damit zwischen dem Spielfeld und den anderen Elementen etwas Platz
bleibt, wählte ich als Tabellenbreite 560 Pixel, dies wurde auch noch auf meinem damaligen Laptop, dessen
Bildschirmauflösung 640x480 betrug, im Browserfenster komplett angezeigt. Aus dem gleichen Grund achtete ich
darauf, dass die Tabelle, oder zumindest das Spielfeld, nicht länger als 320 bis 360 Pixel wurde.
Hierbei kann im Body-Teil eine Hintergrundgrafik, die die Layoutbegrenzung anzeigt, helfen oder auch Schmuckelement
werden, wie man es z.B. auf www.gamecraft.de in
"Springende Punkte", in
"Edelsteine" und anderen sieht.
Bei der Bildschirmauflösung 640x480 ist im Fullscreen-Modus das gesamte Dokument zu sehen.
| Überschrift Anzeige, wer dran ist Zaun als Linkleiste |
Punktestandsanzeige Spielbrett |
Startoptionen Gegner Spielstärke |
| zum Seitenanfang | ||
| zum Seitenende |
Die bunte überschrift entstand mit der "Hackebeil-Methode", indem jeder Buchstabe der überschrift via span und style (Version 2.0) oder font-Attribut (Version 1.0) eine andere Farbe bekam.
<span style="color:#ff5555"><big>R</big></span> <span style="color:#ee5577">E</span> <span style="color:#cc5599">V</span> <span style="color:#aa55aa">E</span> <span style="color:#9955cc">R</span> <span style="color:#7755ee">S</span> <span style="color:#5555ff"><big>I</big></span>
Die Bildanzeige, wer dran ist, besteht aus einem benannten Image, welches den jeweiligen Stein zeigt:
am Zug: <img src="ima0.gif" name="zug" width="24" height="24" alt="dran" border=0>
Die Schaltflächen für Neu, Hilfe u.s.w. wurden als Gartenzaun angelegt, da das Spiel für einen Gartenbauverein war. Eine Latte besteht aus 2 Tabellenzellen. Die erste hat als Bildhintergrund die Zaunfarbe und oben einen schmalen Streifen, der die Zaunlücke darstellt. In dieser Zelle wird der Linktext dargestellt, die Zelle "wächst" mit der Textlänge und die Zaunlücke mit ihr. Die 2.Zelle enthält die Zaunspitze als benamtes Image, um mit mouseover und mouseout Hover-Effekte zu steuern. Bei überfahren des Links soll also in der Zelle neben der, die den Link enthält, die Zaunspitze umgefärbt werden.
<tr>
<td width="160" height="28" class="butt">
<a href="javascript:neu()"
onmouseover="hilite('neu')"
onmouseout="normal('neu')">Neues Spiel</a>
</td>
<td>
<img src="ecke.gif"
width="12" height="24" border="0"
alt="" name="neu">
</td>
</tr>
Ähnlich aufgebaut sind die Verweise für die Funktion neu(), die Funktion hilfe(),
die den Hilfebildschirm als Popup aufruft, und da das Spiel auch im Popup-Fenster gestartet wird, eine Funktion, die das
Spielfenster wieder schließt. Warum? Da ist doch noch das x rechts oben. Ja, aber die Gartenfreunde sind
nicht unbedingt Computerexperten, sondern Leute, denen man in der gleichen Gruppe wie die anderen Elemente,
die zu weiteren Seiten des Vereins oder des Autors führen, auch das Element zum Schließen der Seite
angeben sollte. Die Tabelle für die Verweise/den Gartenzaun bekommt die Eigenschaften
cellpadding="0" und cellspacing="0", so gibt es keine unschönen
Lücken im Zaun.
Warum habe ich nicht die Tabellenzelle in der Zaunfarbe eingefärbt und nur eine schmale Linie als Hintergrund
genommen? - Da gibt es 2 Gründe: die Browser passen die Farben ihrer eigenen Farbtabelle an! Und so gibt es schon
mal einen leichten Schatten bei Bildern, die sich teils aus Grafiken, teils aus einer Browserhintergrundfarbe ergeben.
Obendrein hatten Netscape und der IE4 auch noch andere interne Farbtabellen. - Einigermaßen glatt gehen solche
Mischungen nur, wenn man sich auf die 216 "sicheren" Farben beschränkte. Dies sind Farben des Schemas
#xxyyzz, wobei x, y und z durch 3 teilbar sind, also z.B. #006633 oder #99ccff (c=12, f=15). Diese Farben sind leider
ziemlich knallig und damit nur die wenigsten als Hintergrund brauchbar. Ein guter Kompromiss ist, die Nebenbedingung
"durch 3 teilbar" zu vergessen.
Und warum ist der Zaunpfahl nicht mit CSS entworfen? Warum einfast einfarbiges Bild mit einer einzelnen
hellgrau/dunkelgrauer Doppellinie? - Weil NN4 CSS-Borders nicht oder recht eigenwillig auswertet!
Also gewöhnte ich mir an, zusammenhängende Grafikteile immer mit demselben Werkzeug zu erstellen, das heisst hier: Zaunlatte und Zaunspitze mit Paintshop.
| zum Seitenanfang | ||
| zum Seitenende |
Spiel-Optionen wie Parallelstart oder Diagonalstart, Mensch-Mensch oder Mensch-Computer sowie die Spielstärke
des Computers werden als Radiobuttons innerhalb eines Formulares angelegt. Damit diese Formularelemente mit Javascript
problemlos ausgelesen werden können, bekam das Formular den Namen settings.
Als Action setzt man einen beliebigen String ein, onsubmit="return false" verhindert,
dass eine Action ausgeführt wird.
Wir brauchen die Werte nur an den entsprechenden Stellen im Spiel, vo sie via Javascript ausgelesen werden.
Parallel/Diagonalstart und Erster Zug werden nur beim Start eines neuen Spiels ausgewertet,
der Gegner kann innerhalb des Spiels wechseln, falls z.B. die Schwester auf einmal mitspielen will.
Damit sich die Radiobutton-Gruppen auch visuell voneinander abheben, trennen wir sie mit Linien (<hr>)
ab. Dabei können wir aber nicht einfach die Linien unter die entsprechenden Gruppenelemente setzen, dies
führt zu Lücken in der Mitte. Wir definieren als "Container" eine zweispaltige Tabellenzelle.
<form name="settings" action="dummy" onsubmit="return false">
<table border=0 cellpadding=0 cellspacing=0>
<tr>
<td>Diagonalstart</td>
<td><input type=radio name="diagonal" checked></td>
</tr>
<tr>
<td>Parallelstart</td>
<td><input type=radio name="diagonal"></td>
</tr>
<tr><td colspan=2><hr></td></tr>
<tr>
<td>Tomate beginnt</td>
<td><input type=radio name="start" checked></td>
</tr>
<tr>
<td>Maulwurf beginnt</td>
<td><input type=radio name="start"></td>
</tr>
<tr><td colspan=2><hr></td></tr>
<tr>
<td>2 Spieler</td>
<td><input type=radio name="player" checked></td>
</tr>
<tr>
<td>Spieler/Compi</td>
<td><input type=radio name="player"></td>
</tr>
<tr><td colspan=2><hr></td></tr>
<tr>
<td colspan=2>
Stärke Compi:<br>
<input type=radio name="level" value=1 checked>Doofie<br>
<input type=radio name="level" value=2>Ramscher<br>
<input type=radio name="level" value=3>Aufpasser<br>
</td>
</tr>
</table>
</form>
| zum Seitenanfang | ||
| zum Seitenende |
Vorweg: beim Planen auf Papier erwies es sich als ratsam, in dieser Zelle noch zusätzlich die Punktestandsanzeige unterzubringen. Dies kann folgendermaßen realisiert werden:
<form name="ausgabe" action="dummy" onsubmit="return false"> <img src="ima0.gif" width=24 height=24 alt="Tomate" border=0> <input name="player0" size=3 value=2> </form>
Damit aus ästhetischen Gründen die Punktestand-Anzeige bündig mit den Spielfeldzellen angezeigt wird, brachte ich das Spielfeld und die Anzeige in derselben Tabelle unter.
Das Form-Feld umfasst hier die gesamte Aussenzelle, da nach dem abschließendem Form-Tag die Browser einen ziemlich großen, hier unerwünschten Abstand einfügen. Einen etwas kleineren Abstand fügte ich mit einer Tabellenzeile ein.
Das Spielfeld selbst wird mit einer Javascript-Funktion erzeugt, die an der entsprechenden Stelle des HTML-Dokumentes den Quelltext für das 8x8-Spielfeld einfügt. Damit steht der Inhalt der mittleren Zelle fest:
<form name="ausgabe" action="dummy" onsubmit="return false"> <table border=0 cellpadding=0 cellspacing=0> <tr> <td><img src="ima0.gif" width=24 height=24 alt="Tomate" border=0></td> <td colspan=3><input name="player0" size=3 value=2></td> <td><img src="ima1.gif" width=24 height=24 alt="Maulwurf" border=0></td> <td colspan=3><input name="player1" size=3 value=2></td> </tr> <tr><td colspan=8> </td></tr> <script type="text/javascript" language="javascript" > mach_spielfeld(); </script> </table> </form>
Bei Action wird wieder irgendeine, nicht unbedingt vorhandene Funktion angegeben, der onsumbit-Teil verhindert, dass sie ausgeführt wird. Das Formelement dient nur, die Anzeigen zu manipulieren. Ohne Formelement, d.h. nur mit den input-Feldern streikt NN4 (und einige andere Browser). Die drittletzte Zeile ist ein Beispiel, wie Javascript mitten im Body.Teil eines HTML-Dokument eingebunden werden kann. Der Code wird beim Aufbau des Dokumentes genau an dieser Stelle eingebunden. Dazu müssen sämtliche Parameter, die die Funktion braucht, wie z.B. die Spielfelddimensionen, deklariert sein. Steht der Javascript-Hauptteil im Header oder wird er im Header eingebunden, so ist dies normalerweise sichergestellt.
Aber auch hier spielt NN4 gerne Streiche, häufig geschieht es, dass offline alles korrekt dargestellt wird, aber online fehlen Stücke javascript-generierter Quelltext. Um dies zu prüfen, lässt man sich van NN4 den generierten Quelltext anzeigen. Fehlen wichtige Teile, so sollte man als erstes externen Javascript-Text im Header unterbringen, zumindest die Deklarationen der Konstanten und globalen Variablen. Reicht dies nicht, kann man in einem weiteren Schritt alle Funktionen in den Header schreiben, die zum Aufbau der Seite beitragen. Gleichzeitig sollte man überprüfen, ob der Browser mit dem Stylesheet überfordert ist. Border-Styles und Hintergrundgrafiken z.B. bei Formularen sind bei Problemen zu entfernen, eventuell alle Styles, die sich auf Formelemente beziehen, entfernen.
Damit ist der HTML-Teil des Spiels (fast) fertig.
Der Vollständigkeit halber folgt nun die Funktion, die das Brett erzeugt. Die einzelnen Zellen bestehen aus verweissensitiven Grafiken und sollten in HTML folgendes Aussehen haben:
<a hef="javascript:setzen(xx)"
onmouseover="hili(dran,bild_xx)"
onmouseout="norm(bild_xx)">
<img src="leer.gif" width="24" height="24"
alt="Feld_xx" name="bild_xx" border=0>
</a>
xx steht für eine Laufvariable für das entsprechende Feld. Der Text sollte natürlich lückenlos in einer Zeile stehen, um unschöne Ränder zu vermeiden, kein Problem mit Javascript! Und so sieht der Javascript-Teil aus, der die obige Zeile erzeugt:
function mach_spielfeld()
{ var i,j,k=0,t='',bildname;
for (j=0; j<ymax; j++)
{ t=t+'<tr>';
for (i=0; i<xmax; i++)
{ bildname=&'i_'+k;
t=t+'<td><a hef="javascript:setzen('+k+')'" ';
t=t+'onmouseover="hili(dran,'+bildname+')" ';
t=t+'onmouseout="norm('+bildname+')"> ';
t=t+'<img src="leer.gif" width=24 height=24 alt="Feld '+k+'" ';
t=t+'name="'+bildname+'" border=0>';
t=t+'</a></td>';
k++;
}
t=t+'</tr>';
}
document.writeln(t);
}
Warum ist es wichtig, dass die Images verschiedenen Namen bekommen? Man kann sie doch ebensogut mit
document.images[index] anzusprechen. Im Prinzip ja, funktioniert auch. Aber man sollte aus folgenden
Gründen mit benannten Elementen arbeiten:
Hier wird erst mal mit dem HTML-Teil abgeschlossen, wir haben alle Elemente erzeugt, auf die wir mit Javascript zugreifen müssen. Wa nun folgt, muss nicht im gleichen Dokument stehen, sondern kann ausgelagert werden, so dass man z.B. die Computerstrategie nicht sofort durchschauen kann.
| zum Seitenanfang | ||
| zum Seitenende |
Damit der Bildwechsel des Hover-Effektes flüssig abläuft, sollten die Bilder schon mal über die Internet-Leitung gekommen sein. Dies geschieht mit:
var ima0 =new Image(); ima0.src = "ima0.gif"; var ima0_a=new Image(); ima0_a.src= "ima0_a.gif"; var ima1 =new Image(); ima1.src = "ima1.gif"; var ima1_a=new Image(); ima1_a.src= "ima1_a.gif" var leer =new Image(); leer.src = "leer.gif"; var leer_0=new Image(); leer_0.src= "leer_0a.gif"; var leer_1=new Image(); leer_1.src= "leer_1a.gif"; var ecke =new Image(); ecke.src ="ecke.gif"; var ecke_a=new Image(); ecke_a.src="ecke_a.gif";
Mit var ima0=new Image(); erzeugen wir eine Bildelement, wie sie im HTML-Teil mit <image ... entsteht,
dem wir mit ima0.src="ima0.gif" eins unserer mit Paintshop erstellten Bilder zuweisen.
Bei Ausführen dieser Anweisung marschiert das Bild, falls noch nicht im Cache, vom Server zum Client, voila!
Das Bildelement selbst verschimmelt im weiteren Verlauf des Programms im Hintergrund,
nur dessen Quelle (.src)wird von Zeit zu Zeit angezapft.
| zum Seitenanfang | ||
| zum Seitenende |
Die Funktion zum Einlesen des Hilfetextes sieht folgendermaßen aus (die fürden Ende-Bildschirm ähnlich):
function hilfe()
{ var win2=window.open('hilfe.htm',
'popup''width=560,height=360,scrollbars=auto');
}
Dieser Einzeiler öffnet das Dokument hilfe.htm im Zielfenster namens popup, welches mit der Größe 560x360 initialisiert wird. Man sollte sich sklavisch an diese Syntax halten, ein Leerzeichen zuviel, so wie es bei der Aufzählung der Parameter des neuen Fensters leicht passiert, und die ganze Größenangabe wird ignoriert.
Mit der Benennung des Hifefensters haben wir eine Technik verwendet, die eigentlich dazu gedacht war, benannte
Fenster inerhalb eines Framesets gezielt anzusprechen, es ist das Javascript-Äquivalent zu
target="popup". Existiert dieses Zielfenster nicht, so wird ein neues erzeugt.
Zwar ist unter HTML die saubere Lösung, mit dem reserviertem Ziel target="_blank"
ein neues zu erzeugen.
Aber übergeben wir "_blank" als 2.Parameter an window.open(),
und klickt der Anwender mehrmals auf "Hilfe", so gibt es bei ihm eine Fensterflut.
Das Hilfedokument oder andere Popup-Fenster wie Bestenliste sollten im Body-Tag
onload="this.focus()"
Warum hier der Weg über Javascript? Warum kein ordinärer Link?
Das Hilfefenster sieht ohne Toolbar einfach schicker aus, verdeckt nicht den ganzen Schirm,
und durch Hin- und Herschieben hat man Hilfetext und Spielfeldlayout zusammen im Blickfeld. - Wie man sieht,
sind alle Forderungen, die wir an das Fenster gestellt haben, erfüllt.
| zum Seitenanfang | ||
| zum Seitenende |
... ist mit der einfachste Teil des Projektes, denn alle notwendigen Sachen sind schon erschaffen worden.
Die Zaunspitzen bekamen
individuelle Namen. Deren Grafiken, die Ecken mit und ohne weisse Spitze, sollen bei Bedarf getauscht werden.
Alle benötigten Bilder ecke und ecke_a sind schon vorgeladen, der Hover-Effekt wird dann von den folgenden beiden
functions erledigt, als bildname wird der jeweils vergebene Name der Grafik übergeben:
function hilite(bildname) { document.images[bildname].src=ecke_a.src; }
function normal(bildname) { document.images[bildname].src=ecke.src; }
Diese beiden kleinen Einzeiler übernehmen die ganze Arbeit! Sie bekommen als Parameter den Bildnamen
des jeweils zu ändernden Bildes, wie er im Image-Tag bei name="wasauchimer" angegeben ist,
also onmouseover="hilite('wasauchimmer')".
Bemerkenswert ist hier, dass nicht die Datei,
die die neue Grafik enthält, als Wert von document.images[bildname].src herhalten muss,
sondern die Quelle des schon vorgeladenen Bildesecke.src b.z.w. ecke_a.src.
Die Zeilen für den Bildwechsel im Spielfelt (Cursor-Imitat) soeht fast genauso aus.
Wir fangen an mit der Funktion norm(nr), die das Feld Nr.nr darstellt.
f sei unser Spielfeld, dann bedeutet:
f[nr]=-1: das Feld ist unbesetztf[nr]=0: Spieler 0 besetzt das Feldf[nr]=1: Spieler 1 besetzt das Feldlistenaufbau(dran)) gesammelt werden.
Die ebenfalls noch zu schreibenden Funktion in_liste(nr) gibt an,
ob dieses Feld besetzt werden darf. Wenn ja, wird das rosa oder hellblaue Quadrat angezeigt, je nachdem, wer
am Zug ist, sonst ein neutralgraues Quadrat. Die bereits besetzen Felder zeigen den jeweiligen Spielstein des Spielers:
function norm(nr)
{ if (f[nr]<0)
{ if (in_liste(nr)) // dies ist die Liste mit den erlaubten Zügen
{ if (dran==0) document.images['i_'+nr].src=leer_0.src; // rosa Quadrat
if (dran==1) document.images['i_'+nr].src=leer_1.src; // blaues Quadrat
}
else document.images['i_'+nr].src=leer.src; // neutralgraues Quadrat
}
if (f[z]==0) document.images['i_'+nr].src=ima0.src; // Stein Spieler 0
if (f[z]==1) document.images['i_'+nr].src=ima1.src; // Stein Spieler 1
}
Das globale Array f wird gebraucht zum Protokollieren des Spielstandes.
Eine Funktion, die öfters gebraucht wird, ist das Neuzeichnen des Feldes, ein netter, kleiner Einzeiler.
Er bedient sich an f und norm(nr):
function redraw() { for (var i=0; i<f.length; i++) norm(i); }
Die Funktion hili(dran,nr) ist ähnlich aufgebaut. Nur noch nicht besetzte Felder werden verarbeitet, das halbdurchsichtige Bild ima_a0 oder ima_a1, genauer gesagt,
deren Aussehen soll da erscheinen:
function hili(dran,nr)
{ if (f[nr]<0) // nur nicht besetzte Felder hiliten
{ if (dran==0) document.images['i_'+nr].src=ima0_a.src;
if (dran==1) document.images['i_'+nr].src=ima1_a.src;
// hili abschalten, falls gegen den Computer gespielt wird:
if ((dran==1) && compigegner()) norm(nr);
}
}
Man kann sich jetzt auch vorstelllen, verschieden große Grafiken für den Hover-Efekt zu nutzen. Denn document.images bietet Zugriff auf eine Menge anderen Parameter des Bildes wie z.B. Breite und Höhe. Denen kann man sogar andere Werte unterjubeln. IE macht das auch mit, aber es gibt eine ziemliche Flackerei, wenn der Browser das Layout anpasst. Aber NN4 verweigert schlicht die Zusammenarbeit: nach Laden irgendein Layout neu berechnen? Nicht mit NN4!
| zum Seitenanfang | ||
| zum Seitenende |
Wir haben uns oben das Formular namens ausgabe
mit den Input-Feldern player0 und player1 erstellt
und das Formular settings mit den Radiobutton-Gruppen
diagonal, start, player und level.
Angesprochen werden die Formularelemente in Javascript dann mit
document.form[i].elements[j]document.form['formname'].elements['elementname']document.formname.elementname
Variante 1 ist nicht sehr pflegeleicht, und von den Bildern her weiss ich, dass
IE4 und NN4 so ihre ganz eigene Zählweise haben.
Variante 2 nehme ich gerne, wenn ich große Formulare habe und deren Elementnamen
systematisch vergeben habe.
In diesem Spiel tut es Variante 3 voll und ganz.
An player0 und player1 interessiert uns die Eigenschaft
value, an der Radiobuttongruppe die einzelnen Elemente, die wie ein
Array mit dem Startindex 0 angesprochen werden, und deren Eigenschaft checked,
bei der letzten Gruppe auch value.
Und so sehen die Zugriffe aus:
playerxx im Formular ausgabedocument.ausgabe.player0.value=was_auch_immer; document.ausgabe.player1.value=der_zweite_wert;
Analog geht der Zugriff auf Radiobuttongruppen-Elemente. Allerdings muss hier das einzelne Element des
Arrays auf checked geprüft werden, es gibt keine "abgesegnete" Möglichkeit,
sofort den gecheckten Index zu erhalten. Wahrscheinlich wurden Checkboxes und Radiobuttons
javascript-mäßig in einen Topf geworfen.
Einfach geht es noch, wenn die Gruppe nur 2 Elemente enthält. Ist eins nicht gecheckt, ist es das andere
zwangsweise, denn wir initialisieren ja brav alle Formularwerte mit den gängigsten Spieloptionen.
settings
parallelstart =document.settings.diagonal[1].checked;
spieler1_beginnt=document.settings.start[1].checked;
computergegner =document.settings.player[1].checked;
strategie=-1;
for (var i=0; i<document.settings.level.length; i++)
if (document.settings.level[i].checked)
strategie=document.settings.level[i].value;
| zum Seitenanfang | ||
| zum Seitenende |
Diese Funktion heisst bei mir standardmäßig neu(), mit oder ohne Parameter,
je nachdem, was alles gemacht werden soll. neu()muss hier nacheinander folgendes erledigen:
Das Brett sind visuell die Zellen der Tabelle im mittleren Feld, zum Protokollieren legen wir ein
Array fan. Brett leeren heisst: alle Werte mit -1 füllen. Stein von Spieler 0 setzen bedeutet:
das Feld bekommt den Wert 0, bei Spieler1 den Wert 1.
Diese müssen nun, je nachdem, ob Diagonalstart oder Parallelstart gewünscht ist, belegt werden.
Dargestellt wird jetzt noch nichts.
count=0;
for (i=0; i<f.length; i++) f[i]=-1;
f[27]=0;
f[28]=1;
if (document.settings.diagonal[1].checked)
{ f[35]=0;
f[36]=1;
}
else
{ f[35]=1;
f[36]=0;
}
punkte();
Die Steine sind gesetzt, jetzt kann die Anzeige aktualisiert werden. Dazu werden die Steine der Spieler gezählt und deren Zahl angezeigt. Die erledigt folgende kleine Funktion, die auch während des Spiels ihre Dienste verrichten muss:
function punkte()
{ var sum0=0;
var sum1=0;
for (var i=0; i<f.length; i++)
{ if (f[i]==0) sum0++;
if (f[i]==1) sum1++;
}
document.ausgabe.player0.value=sum0;
document.ausgabe.player1.value=sum1;
}
Die globale Variable dran speichert, wer gerade am Zug ist.
if (document.settings.start[1].checked) dran=1;
else dran=0;
Es wird durch Bildwechsel bei document.zug angezeigt, wer dran ist. Auch diese Funktion muss
im Spielverlauf mehrmals herhalten:
function zeigedran(dran)
{ if (dran==0) document.zug.src=ima0.src;
if (dran==1) document.zug.src=ima1.src;
}
Für den Spieler dran werden die möglichen Züge in einer Liste gesammelt, die im nächsten
Abschnitt "KI die erste" beschrieben wird, dann endlich wird das Spielfeld gezeichnet:
zeigedran(dran); listenaufbau(dran); redraw();
Last noch least wird entschieden, ob der Computer einen Zug machen soll:
if ((dran==1) && (document.settings.player[1].checked)) compimove(); else aktiv=true;
Die globale Variable aktiv bestimmt, ob der Spieler ins Brett klicken darf oder
nicht. Damit wird Chaos verhindert, während der Computer an der Reihe ist.
So, jetzt noch den Function-Header mit der öffnenden Klammer und der Variablendeklaration für i obendrüber,
die schließende Klammer untendrunter, - und feddich!
Und weil's zum Thema Formularauswertung passt, folgt nun auch noch die Ende-Funktion, die je nach Endstand ein anderes Dokument in einem Popup anzeigt. Hier wird eine Variante gezeigt, wie man auf verschachtelte Elemente zugreifen kann, ohne gepunktete Bandwürmer zu erzeugen:
function ende()
{ var i,nr;
punkte();
with(document.ausgabe) i=player1.value-player0.value;
if (i<0) nr=0; // Spieler0 hat gewonnen
else if (i==0) nr=2; // unentschieden
else nr=1; // Spieler1 hat gewonnen
var win2=window.open('ende'+nr+'.htm','popup',
'width=560,height=360,scrollbars=auto');
}
Erst werden schnell noch mal die Punkte berechnet, dann gecheckt, wer mehr hat, bevor der entsprechende Ende-Bildschirm aufgerufen wird.
Hiermit sind alle Functions erstellt, die mit den HTML-Elemente interagieren sollen. Was nun folgt,
lässt sich 1:1 in andere Sprachen übernehmen. Ab jetzt können wir uns (fast) ganz der Spieletheorie widmen.
Ich trenne bei größeren Projekten immer zwischen Darstellung/Interaktion und restlichen Funktionen.
Die Funktionen zur Interaktion mit HTML-Elementen wurden im Laufe der Zeit ausgelagert in die Crossbrowser-Bibliothek,
ohne die ein großer Teil der Gamecraft-Spiele nicht mehr auskommt.
Und gibt es mal wieder ein neues DOM, so werden die Funktionen der Bibliothek ergänzt, statt 50 - 70 Spiele zu
durchforsten und umzuschreiben.
| zum Seitenanfang | ||
| zum Seitenende |
Zum Anzeigen des Spielfeldes muss bekannt sein, auf welche Felder der Spieler, der am Zug ist, setzen kann. Die Regeln zum Setzen des Steins sind folgendermaßen:
In diesem Anschnitt werden die ersten beiden Punkte besprochen.
Die Bedingung für das Feld, in das zu setzen ist, ist also: es muss frei sein, und daneben ist mindestens ein gegnerischer Stein. Der kann rechts davon, links, oben, unten, rechts oben, links oben, links unten oder rechts unten sein. Ausserdem muss irgendwo dahinter ein eigener Stein sein. Die Funktion, die also berechnet, ob und wieviel Steine man durch diesen Zug gewinnt, sieht folgendermaßen aus:
function checkmove(dran,x,y)
{ var gain=0;
gain=gain+rechts(dran,x,y,false);
gain=gain+links(dran,x,y,false);
gain=gain+oben(dran,x,y,false);
gain=gain+unten(dran,x,y,false);
gain=gain+linksoben(dran,x,y,false);
gain=gain+rechtsunten(dran,x,y,false);
gain=gain+linksunten(dran,x,y,false);
gain=gain+rechtsoben(dran,x,y,false);
return gain;
}
Der Zug ist gültig, wenn gain mindestens 1 ergibt. rechts(dran,x,y,flag) checkt,
ob nach rechts Steine zu gewinnen sind, links(dran,x,y,flag), ob links was zu holen ist u.s.w.
flag=false bedeutet, dass der Zug nur gecheckt werden soll, bei flag=true
wird er dann auch ausgeführt. Zum Anzeigen der Züge z.B. steht flag auf false.
Die Listen sind als counted arrays angelegt: das erste Element enthält die Anzahl der Daten,
dann folgen nacheinander die Daten. - push und pop verbieten sich hier, weil die
Listen m und g über ihre Indices verbunden sind: Zum Zug m[3]
gehört der Gewinn g[3].
Die Liste der mögliche Züge wird also aufgebaut, indem jedes freie Feld gecheckt wird, ob man mit ihm
punkten kann. Für die Computerstrategie wird gleich gespeichert, wieviele Gegner man mit den Zug umdrehen kann
(g).
Die 2.Funktion checkt einfach, ob ein bestimmter Wert in der Move-Liste vorkommt.
// ----- Listenauswertungen: ----------
function listenaufbau(dran)
{ var c,i,j,k=0;
m[0]=0; // Moves-Liste initialisieren
g[0]=0; // Gain-Liste initialisieren
for (j=0; j<ymax; j++) for (i=0; i<xmax; i++) if (f[k]<0)
{ c=checkmove(dran(i,j));
if (c>0)
{ m[0]++; m[m[0]]=k; // Koordinate anfügen
g[0]++; g[g[0]]=c; // Gain mit dieser Koordinate
}
k++;
}
}
function in_liste(nr)
{ var i,ok=false;
if (m[0]>0) for (i=1; i=<m[0]; i++) if (nr==m[i]) ok=true;
return ok;
}
Kommen wir nun zu den Funktionen rechts(dran,x,y), links(dran,x,y), u.s.w..
Das Erstellen ist Knochenarbeit mal 8! Muss aber gemacht werden. Weil sich bei den Bedingungen schnell
Fehler einschleichen, und die sowieso für alle 8 Himmlesrichtungen anders sind, empfiehlt es sich,
auch 8 verschiedenen Funktionen dafür schreiben. Die einzelne Funktion sieht dann nicht mehr ganz so wüst aus.
Als Beispiel sei das Entwickeln hier für rechts(dran,x,y) und linksunten(dran,x,y)
gezeigt:
rechts(dran,x,y,setzen)
function rechts(dran,x,y,setzen)
{ var k,posi=x+y*xmax,gain=0;
var gegner=(dran+1)%2; // - Gegner bestimmen
// da mindestens der letzte Stein ein eigener sein muss
// und der davor ein gegnerischer, muss das ausgesuchte Feld
// mindextens 2 Felder vom Rand entfernt sein.
// Der rechte Rand hat die x-Koordinate (xmax-1), also ist
// die höchste erlaubte x-Koordinate (xmax-3). Zusätzlich
// muss der Stein mit der Koordinate (x+1) dem Gegner gehören:
if (x<(xmax-2)) if (f[posi+1]==gegner)
{ k=1; // das wäre dann der erste gegnerische Stein
// k wird so lange hochgezählt, bis mit (x+k) ein eigener Stein
// oder der Rand erreicht wird:
while ((f[posi+k]==gegner) && ((x+k)<(xmax-1))) k++;
// falls der letzte Stein ein eigener war, wird eingesackt:
if (f[posi+k]==dran)
{ gain=gain+k-1;
if (setzen) // falls gewünscht, Spielfeld f updaten:
{ k=1;
while ((f[posi+k]==gegner) && ((x+k)<(xmax-1)))
{ f[posi+k]=dran;
k++;
}
}
}
}
return gain;
}
Bei linksunten(dran,x,y,setzen) muss als erstes abgecheckt werden,
ob der Stein weit genug von beiden Rändern (x=0) oder (y=ymax-1) liegt.
Wenn ja, muss der Stein (x-1)(y+1) dem Gegner gehören.
Liegt der Stein direkt eine Reihe tiefer,
so ist seine linearisierte Koordinate posi+xmax,
das zu untersuchenden Feld ist also posi-1+xmax,
das der ganzen Diagonale posi-k+k*xmax.
Beim Auftreffen auf den ersten Rand ist abzubrechen, der Rest ist wie bei der obigen Funktion.
linksunten(dran,x,y,setzen)
function linksunten(dran,x,y,setzen)
{ var k,gain=0,posi=x+y*xmax,gegner=(dran+1)%2;
if ((x>1) && (y<(ymax-2))) if (f[posi-1+xmax]==gegner)
{ k=1; // s.o.: einen hamma dann schon!
while ((f[posi-k+k*xmax]==gegner) && ((x-k)>0) && ((y+k)<(ymax-1))) k++;
if (f[posi-k+k*xmax]==dran)
{ gain=gain+k-1;
if (setzen)
{ k=1;
while ((f[posi-k+k*xmax]==gegner) && ((x-k)>0) && ((y+k)<(ymax-1)))
{ f[posi-k+k*xmax]=dran;
k++;
}
}
}
}
return gain;
}
Die anderen 6 Himmelsrichtungen sind die gleiche Knochenarbeit, die ich jetzt mal keinem abnehmen will ;-).
| zum Seitenanfang | ||
| zum Seitenende |
Punkt 1 und 2 sind abgehakt mit dem vorigen Abschnitt. Also sind jetzt Punkt 3 und 4 dran.
Wenn ein Spieler an der Reihe ist, wird
aktiv=true freigeschaltet,
dann so lange gewartet, bis ein Feld, was in dieser Liste enthalten ist, angeklickt wird.f, die Anzeigen aktualisiert, der Zugcounter hochgesetzt.dran wechselt, die Liste für den anderen Spieler wird aufgestellt, das Spielfeld angezeigt| zum Seitenanfang | ||
| zum Seitenende |
... wird erledigt von der Funktion setzen(x,y). Bevor diese aber auch nur einen Finger rührt,
wird gecheckt, ob überhaupt ins Spielfeld geklickt werden durfte (die globale Variable aktiv).
Diese kleine Abfrage verhindert viel Herzeleid, wenn der Anwender nicht abwarten kann, und einfach durch unkontrolliertes Herumklicken mehrere Computerzüge gleichzeitig in Gang setzt, die den Browser gnadenlos an seinen
Rekursionsversuchen verrecken lassen.
Die Funktion umdrehen(dran,x,y) ruft die ganzen Himmelsrichtungs-Funktionen dann mit dem Flag
true auf, was den Zug im Feld f ausführt.
Feld f wird dargestellt,
die Punkte summiert und das Feld angezeigt, und der nächste ist dran:
setzen(x,y)
function setzen(x,y)
{ if (aktiv)
{ var z=x+y*xmax;
if (in_liste(z))
{ umdrehen(dran,z);
count++;
punkte();
redraw();
spielerwechsel();
}
if (dran==1)
{ if (document.settings.player[1].checked) setTimeout("compimove()",1000);
}
}
}
Was soll das mit dem Timeout?
Der Computer reagiert manchmal so schnell, dass man es nicht mitbekommt. Und man will doch wissen,
warum plötzlich fast alle Steine blau sind! ;-)
umdrehen(dran,z)
function umdrehen(dran,z)
{ // Konversion Linearkoordinaten in 2dim:
var x=z%xmax,y=Math.floor(z/xmax);
rechts(dran,x,y,true);
links(dran,x,y,true);
oben(dran,x,y,true);
unten(dran,x,y,true);
linksoben(dran,x,y,true);
rechtsunten(dran,x,y,true);
linksunten(dran,x,y,true);
rechtsoben(dran,x,y,true);
f[z]=dran;
}
| zum Seitenanfang | ||
| zum Seitenende |
Diese Funktion
dran,
Die ganzen verwendeten Funktionen wurden oben bereits erklärt mit Ausnahmen des compimove(), der im nächsten
Kapitel der Hauptdarsteller ist.
Der Wechsel von dran vollzieht sich nach folgendem Algorithmus, der verwendet werden kann, wenn reihum n Spieler
(Nr. von 0 bis n-1) zum Zuge kommen sollen: dran=(dran+1)%n. Im Klartext sieht das Ganze so aus:
spielerwechsel()
function spielerwechsel()
{ dran=(dran+1)%2; // allg.Algo für "Ringe" der Größe n
zeigedran(dran); // Kap. 2.5.
listenaufbau(dran); // Kap. 3.1.
redraw(); // Kap. 2.3.
if (m[0]<1)
{ alert('Spieler '+dran+' muss aussetzen!');
dran=(dran+1)%2;
zeigedran(dran);
listenaufbau(dran);
redraw();
if (m[0]<1) ende(); // Kap.2.5.
else
{ if ((dran==1) && document.settings.player[1].checked) compimove();
}
}
}
Was muss nun die Funktion compimove() alles leisten? Sie muss:
aktiv=false;,compimove()
function compimove()
{ var zug,t,strat=get_strat();
var params=new Array();
aktiv=false;
// getopt liefert 2 Werte, durch p getrennt
// als String - dieser Umweg ist nötig,
// weil function eigentlich nur 1 Wert
// zurückliefern kann:
t=getopt(dran,strat);
params=t.split('p'); // am p aufsplitten
zug=params[0]; // Zug ist in params[0]
if (zug>-1)
{ umdrehen(dran,zug);
count++; // Zugcounter hochzählen
redraw(); punkte();
}
aktiv=true; spielerwechsel();
}
function get_strat() // vgl.Kap.2.4.
{ var i,t=0;
with (document.settings)
{ for (i=0; i<level.length; i++)
if (level[i].checked) t=level[i].value;
}
return t;
}
Der Computer stellt uns mittlerweile das Spielfeld bereit, setzt die ersten Steine je nach Spieloption,
ermittelt den Spielstand und ist strenger, aber gerechter Schiedsrichter (Ringrichter?) für zwei Spieler.
Das "Sahnehäubchen" dass er selbst mitspielt, geht aus von der Funktion compimove(), die den Zug nach der gewählten Strategie aussucht und durchführt.
| zum Seitenanfang | ||
| zum Seitenende |
Wie kann man nun einem Computer beibringen, Reversi zu spielen?
Das Wichtigste, die Regeln hat er schon begriffen, als Gegner könnte er sich jetzt irgendeinen der in der Liste gesammelten Zugmöglichkeiten aussuchen:
my_move=Math.floor(m[0]*Math.random())+1; my_move=m[my_move];
... und fertig ist die Laube! Für den Anfänger in diesem Spiel ist er damit der ideale Gegner. Leider macht es dem versierten Reversi-Spieler keinen Spaß, gegen so einen "Dummy" zu spielen.
Ein anderer Algorithmus muss her: möglichst viele Punkte einsacken. Auch diese Strategie ist ruckzuck fertig, denn in g wurden die Anzahl der umgedrehten Gegner des entsprechenden Zuges erfasst. Man
nimmt den Zug m, dessen g am höchsten ist.
my_move=m[1];
my_wert=g[1];
if (m[0]>1) for (i=2; i<=m[0]; i++)
{ if (g[i]>my_wert)
{ my_move=m[i];
my_wert=g[i];
}
}
Schon besser, und für viele Spiele auch eine recht brauchbare Strategie. Aber wer schon länger Reversi spielt, weiss, dass man solche "Ramscher" schnell ins Messer laufen lassen kann. Trotzdem ist es in bestimmten Phasen des Spiels die beste, so dass ein ausgefeiltes Computerprogramm in dieser Phase auf diese Strategie umschaltet.
Die beiden oben genannten Strategien haben bei langsamen Systemen, zu denen ein Browser mit einem Javascript-Interpreter nun mal zählt, ihre Daseinsberechtigung. Für einen Reversi-Freak sind sie aber bei weitem nicht ausreichend. Die weiter unten erläuterte Strategie fand hier zum erstenmal Anwendung auf einem C-64, sie wurde auf einem System mit Turbo-Pascal verfeinert.
Wer schon etwas länger Reversi spielt, weiss, dass das Besetzen einiger Felder wie z.B. der Ecken äußerst erstrebenswert ist, wohingegen die Felder direkt davor höchste Gefahr bedeuten, weil man es so dem Gegner ermöglicht, diese zu besetzen.
Die Erfahrung, die man gemacht hat, lässt sich darstellen durch ein Wertefeld, in dem man z.B. den einzelnen Plätzen die Wertung 9999 (wenn's eben geht, besetzen) bis 1 (unbedingt vermeiden) gibt. Dieses Feld könnte etwa so aussehen:
w[i]| 9999 | 5 | 500 | 200 | 200 | 500 | 5 | 9999 |
| 5 | 1 | 50 | 150 | 150 | 50 | 1 | 5 |
| 500 | 50 | 250 | 100 | 100 | 250 | 50 | 500 |
| 200 | 150 | 100 | 50 | 50 | 100 | 150 | 200 |
| 200 | 150 | 100 | 50 | 50 | 100 | 150 | 200 |
| 500 | 50 | 250 | 100 | 100 | 250 | 50 | 500 |
| 5 | 1 | 50 | 150 | 150 | 50 | 1 | 5 |
| 9999 | 5 | 500 | 200 | 200 | 500 | 5 | 9999 |
Dieses Feld ist hoch symmetrisch (2 senkrecht aufeinanderstehende
Spiegelachsen), es reicht, nur ein Viertel zu belegen und den Rest
erstellen zu lassen. Theoretisch ginge es auch, nur ein "etwas
dickeres" Achtel hinzuschreiben, aber der Algorithmus zum "Ausbreiten"
über das ganze Feld frisst diesen Vorteil wieder auf.
Der Computer kann diese Tabelle als Lookup-Table benutzen, um den Wert eines zu besetzenden Feldes
zu erkennen.
In dieser Strategie wird der einzelne Zug nach dem größten strategischem Gewinn ausgesucht. Es wird der Zug genommen, der die meisten strategischen Punkte laut Wertefeld ergibt.
function getmax(dran)
{ var i,j,sum,max;
// Hilfsfeld zum Speichern des aktuellen Spielstandes
// Da Javascript-Rekursionen auf weitaus wackligeren Beinen
// stehen als die anderer Programmiersprachen,
// ist dieser ümweg nötig
var f0=new Array();
var gegner=(dran+1)%2; // vgl. Kap.3.1.
max=-999999; // bester zu erreichenden Wert,
// wird erst mal möglichst niedrig
// angesetzt, damit auch ein Zug
// ausgewählt wird
var zug=-1;
listenaufbau(dran);
if (m[0]>0)
{ // aktuellen Spielstand speichern, SNA!
for (j=0; j<f.length; j++) f0[j]=f[j];
for (i=1; i<=m[0]; i++)
{
// Versuch durchführen:
umdrehen(dran,m[i]);
// Bewertung des Versuches:
// wer steht danach besser da?
// Weil die Stellung bewertet wird,
// werden nicht einfach die Steine gezählt,
// sondern deren Positionswerte addiert
sum=0;
for (j=0; j<f.length; j++)
{ if (f[j]==dran) sum=sum+w[j];
if (f[j]==gegner) sum=sum-w[j];
}
// eigener Zug ist Goldes wert,
// das Einfügen dieser Bewertung
// erwies sich als günstig
sum=sum+10*w[m[i]];
// besten Zug merken:
if (sum>=max) { zug=m[i]; max=sum; }
// aktuellen Spielstand wiederherstellen:
for (j=0; j<f.length; j++) f[j]=f0[j];
}
}
return zug+'p'+max; // ümweg, um 2 Werte zurückzugeben
}
Dies als Beispiel, wie so ein Wertefeld eingesetz werden kann. Denkbar sind bestimmt noch etliche andere Varianten. Allen diesen Ansätzen ist gemein, dass die Erfahrung, die man gemacht hat, in dieses Wertefeld einfließen. Ein ganzer Zweig der Mathematik, die Spieltheorie, befasst sich mit solchen Ansätzen.
Was soll das SNA hinter aktuellen Spielstand speichern? - SNA heist "[S]o und [n]icht [a]nders!". Man könnte auf die Idee kommen, dass man die von anderen Sprachen gewohnte, elegante Syntax wie f0:=f; einsetzen kann, schaut man sich die Werte von f und f0 danach an, so scheint es auch den gewünschten Effekt zu haben. Ändert man dann allerdings einen Wert in f, so ist er auch in f0 geändert. f und f0 stehen hier nicht für die Daten selbst, sondern sind Zeiger darauf.
Man kann sich das Ganze ungefähr so vorstellen: da ist das weite Land Amerika (Speicher, RAM), in diesem gibt es Menschen (Objekt-Daten), und diese kleinen Plastikkärtchen wie Kreditkarten, die Driver's Licence und die Social Security Number (Zeiger, Referenzen auf diese Subjekte, äh Objekte). Wer mal in Amerika war, weiss, du bist ein Nichts ohne Kärtchen! Die Kärtchen werden gebraucht, wenn du mit Scheck bezahlst, zu Behörden gehst u.s.w., kurz, man identifiziert dich daran.
Und f0=f verpasst den f-Daten zur schon vorhandenen Referenz noch eine weitere Referenz (die Daten haben z.B. eine Driver's Licence und eine Mastercard). Schlägt dir einer wegen deiner Driver' Licence die Zähne ein, so fehlen sie dir auch als Inhaber der Master-Card. Und löscht man die Driver's Licence (nach 5 Jahren, entspricht dem Löschen eines Zeigers), so kanst du dich doch noch behaupten dank deiner Mastercard (ein Zeiger zeigt noch auf die Daten). Wenn diese allerdings auch noch eingezogen wird, d.h. der letzte Zeiger auf dich auch noch verschwindet, so bist du eine ganz arme Sau.
Mit der obigen Syntax greifen wir gezielt auf die einzelnen (primitiven) Daten zu und duplizieren diese. Um in der Metapher zu bleiben, danach ist es nicht mehr ein- und dieselbe Person mit Driver's Licence und Mastercard, sondern 2 verschiedene Personen (Objekte), eine identifiziert sich mit Driver's Licence, die andere mit Mastercard.
In der Spieletheorie begegnet man häufiger dem Begriff "Spielbaum"
oder auch "Entscheidungsbaum". Dies ist nichts anderes als die
grafische Aufzeichnung, wie ein 2-oder Mehrpersonenspiel abläuft. Man
hat eine bestimmte Ausgangssituation auf dem Brett, der als hier als
schwarzer Kreis angezeigt und mit 0 markiert ist. Der
Spieler, der gerade dran ist (Spieler Schwarz), hat eine bestimmte
Anzahl Zugmöglichkeiten, die zu neuen Situationen auf dem Brett führen
(rote Kreise in der Ebene darunter). Von diesen neuen Situationen aus
kann der zweite Spieler (Spieler Rot) wiederum zwischen einigen Zügen
wählen, was erneut zu einer weiteren Ebene mit etlichen (schwarzen)
Kreisen für die neuen Spielsituationen für Spieler Schwarz führen.
Dieses Verfahren kannn man rein theoretisch weiterführen, bis einer der
beiden Spieler gewonnen hat. Ziel der Spieler ist es dann, jeweils den
Zug einzuleiten, der zum Sieg oder zumindest zum Unentschieden führt.
Das Ganze sieht wie ein umgekehrter Baum aus (zumindest aus Sicht der Mathematiker).
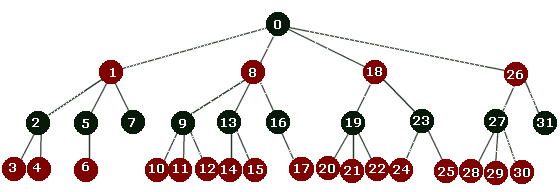
Die Kreise, die die Platzhalter für die Spielsituationen sind,
werden Knoten (Nodes) genannt, ein spezieller Knoten ist hier die 0
für die Ausgangsstellung, Wurzel (root) genannt, und alle Knoten, von
denen aus kein Zug mehr möglich, d.h. das Spiel zu Ende ist. Diese
nennt der Mathematiker Blätter (leafs). Um die Beschreibung komplett zu
machen, nennt man die Linien von einem Spiel(zu)stand zum anderen, den
Zug, Kante, und last not least bezeichnet man die Reihen roter und
schwarzer Kreise als Ebenen.
Diese Knoten haben bestimmte Werte für Rot oder Schwarz. Man berechnet sie aus den erreichbaren Blättern. Dabei wird angenommen, dass jeder Spieler die für sich optimale Strategie anwendet.
| Spielbaum: | Darstellung möglicher Spielzüge in Form eines umgekehrten Baumes |
| Knoten: | eine beliebige Spielsituation im Spielbaum, auch node genannt |
| Wurzel: | Ausgangssituation im Spielbaum, auch root genannt |
| Blatt: | Endsituation im Spielbaum, auch leaf genannt, von hier aus sind keine weiteren Züge möglich |
Dazu betrachten wir uns das Spiel aus der Sicht von Schwarz, der am Zug ist.
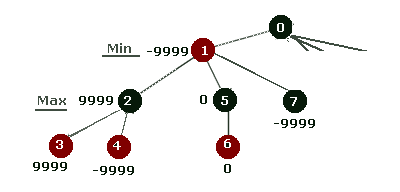
Ist z.B. einer der Knoten 3 oder 4 eine Gewinnsituation (9999 für Schwarz) so erhält der Knoten 2 diesen Wert, da Schwarz von dieser Spielsituation aus gewinnen kann. Schwarz wird immer auf den Knoten mit dem höchsten Wert ziehen. Der Wert wird also "hochgereicht". Die gleiche überlegung kann man nun für alle Blätter anstellen, und man erhält die Werte der darüberliegenden Knoten. So enthält Knoten 5 den Wert von Knoten 6, sagen wir, 0 fü Unentschieden, Knoten 7 ist selbst ein Blattknoten mit z.B. einem Endwert -9999 (Schwarz verliert).
Rot hat von Knoten 1 aus die Chance, zu 2 mit dem Wert 9999 (Schwarz gewinnt), zu 5 mit dem Wert 0 oder zu 7 mit dem Wert -9999 (Schwarz verliert) zu gelangen. Um zu gewinnen, wird Rot von 1 aus nach 7 ziehen. Rot wird immer zu dem Knoten mit dem geringsten Wert ziehen. Knoten 1 erhält also durch Rot den Wert -9999 (= ist für Schwarz zu vermeiden).
Diese Berechnung ist für alle Knoten durchzuführen, wobei die schwarzen den größte Wert der nächsttieferen Ebene annehmen, die roten die kleinsten.
Und wie erhält man nun den Wert der Blattknoten? - Indem man die Spielzüge bis zum bitteren Ende simuliert und bewertet! Dass das in Arbeit ausarten kann, sieht man schon an dem Diagramm, bei dem der Wert der Stellung auf dem Brett für jeden dieser Knoten berechnet werden muss.
Der Minimax-Algorithmus besagt, dass abwechselnd von Ebene zu Ebene des Entscheidungsbaumes einmal der minimale Wert, einmal der maximale Wert des Knotens der tieferen Ebene "weitergereicht" wird.
Die Werte werden letzendlich in der Endstellung (Blattknoten) durch die Bewertungsfunktion berechnet.
Im Programm selbst wird das mit den Vorzeichen der Werte geregelt, die von Ebene zu Ebene wechseln. Dies ist möglich, weil die Bewertungsfunktion mit verschiedenen Vorzeichen für dran und gegner arbeitet.
Damit die Funktion getmax "blattknotenberechnungstauglich" wird, muss man sie mit ein wenig Code erweitern, denn bisher berechnet sie die Stellungen nur für mögliche Züge. Gegen Ende kann es allerdings auch mal vorkommen, dass einer der Spieler nicht ziehen kann. Auch in diesem Fall muss ein Wert hochgereicht werden. Die Berechnungsfunktion wird "ausgelagert, da sie an 2 verschiedenen Stellen mit unterschiedlichem Ziel aufgerufen wird. Zudem empfiehlt es sich, den Anfangswert der Bewertung global vorzubelegen, da sie in 2 Funktionen gebraucht werden. Zu schnell hat man sich vertippt, und es kann passieren, dass ungültige Züge weiterverfolgt werden und, wenn der Computer verliert, dazu führt, dass er keinen Zug mehr ausführt.
getmax und Bewertungsfunktion
function getmax(dran)
{ var i,j,sum,max,zug;
var gegner=(dran+1)%2;
max=minimum;
var zug=-1;
listenaufbau(dran);
if (m[0]>0)
{ for (j=0; j<f.length; j++) ff[0][j]=f[j];
for (i=1; i<=m[0]; i++)
{ umdrehen(dran,m[i]); // Zug virtuell ausführen
// besten Blattknoten suchen und bewerten:
sum=bewerten(dran);
if (w[m[i]]>1) sum=sum+10*w[m[i]];
if (sum>=max) { zug=m[i]; max=sum; }
for (j=0; j<f.length; j++) f[j]=ff[0][j];
}
}
// Blattknoten berechnen, wenn kein Zug möglich
else max=bewerten(dran);
return zug+'p'+max;
}
// Bewertungsfunktion:
function bewerten(dran)
{ var i,sum=0,gegner=(dran+1)%2;
for (i=0; i<f.length; i++)
{ if (f[i]==dran) sum=sum+w[i];
else if (f[i]==gegner) sum=sum-w[i];
}
return sum;
}
Damit der Computer mit seiner Rechnerei nicht so lange beschäftigt ist, breche ich hier die Minimax-Suche nach einer bestimmten Zahl von Ebenen ab. Da man hier meist noch keinen Endzustand findet, müssen die Blattknoten neu definiert werden: es sind die Knoten, an denen die Simulation der Züge abbricht. Deren Werte berechnen sich aus dem Wertefeld für die beste strategische Position. Hat der Spieler, der am Zug ist, dort einen Stein, wird dessen Wert addiert, steht da der Stein des Gegners, wird dessen Wert subtrahiert. (vgl.Bewertungsfunktion)
Man hat an dieser Stelle zwar nicht den Weg zu einer gewinnenden Position, aber doch die (hoffentlich) beste Ausgangsposition dafür.
Diese simple, kleine rekursive Prozedur ließ sich in Turbo-Pascal 3 6x aufrufen (Quelltext vom 5.5.1988, Düsseldorf, Aachen), beim 7.Mal gab es einen Stack overflow. Kick-Pascal war in der Hinsicht freundlicher, allerdings wurden die Rechenzeiten sogar auf damals einem der schnellsten Home-Computer bei Tiefen>7 unerträglich, so dass damals als Maximalstufe 6 gewählt wurde, was aber als Herausforderung voll und ganz ausreichte.
Und Javascript? Auch beim besten Optimieren ist mehr als Stufe 3 nicht drin!
Dieser Algorithmus brachte im ersten Anlauf, einer 1:1-Umsetzung des Pascal-Programms, gnadenlos jeden Javascript-Interpreter zum Absturz: Entweder gab es schon bei Tiefe 2 einen saftigen Stack overflow (IE), oder es rührt sich gar nichts mehr (NN). Grund: In Pascal konnten Schritt 4 und 5 sowie 6.5 weggelassen werden, indem man das jeweilige Feld als "Call by value" übergab. Und die Umsetzung war zunächst 1:1! D.h.ich verließ mich darauf, dass Variable in Javascript durch "Call by value" übergeben werden. Die Objekt-Werte wie z.B. Array-Werte einer Javascript-Funktion hingegen werden übergeben durch einen "Call by reference"-Mechanismus. Dieser umständliche Wortlaut deshalb, weil die Javascript-Puristen behaupten, auch diese werden eigentlich durch "Call by value" weitergegeben. Hier spaltet sich das Objekt auf in Objektreferenz (Identifikation) und Daten (Eigenschaften). Die Referenz/Identifikation bleibt, die Daten/Eigenschaften ändern sich, also ein "Call by reference". Ohne die vorigen Arrays für das Spielfeld und die Zugliste zu kopieren, endete die Funktion erst mal in einem heillosen Durcheinander. (vgl.oben, es wurde also nur die Social Security Card ans Unterprogramm weitergereicht)
Die Abhilfe also: die Datenfelder werden von vorneherein deklariert (viele verschiedene Social Security Cards bereitgestellt), so dass es auf die Kapselung nicht mehr so ankommt. - Aus den bisher eindimensionalen Arrays für die Zugliste und das Spielfeld werden 2-dimensionale, die 2. Dimension gibt die jeweilige Suchtiefe an, deren
Maximalwert erst mal mit 6 (Angestellten) angegeben wird. Da die Funktionen listenaufbau() und umdrehen(nr,dran) immer auf m und f arbeiten (Karten der Watschenmännchen), werden die Ausgangszustände der jeweiligen Rekursion auf ff[tiefe] und mm[tiefe] gesichert (die Leute mit diesen Karten sind das Ersatzteillager fürs Watschenmännchen). Da wir hier mit Tiefensuche arbeiten, kommen wir pro Tiefe mit einem Backup-Feld (Ersatzteillager) aus.
minimum=-999999; // zusätzliche Globale
tmax=6; // Anzahl Felder und Vektoren
var count=0; // Zugzähler
var ff=new Array(); // Backup-Feld fuer Rekursion
var mm=new Array(); // Backup-Liste fuer Rekursion
for (i=0; i<tmax; i++)
{ ff[i]=new Array();
mm[i]=new Array();
}
Und siehe da, die folgende Funktion lief problemlos durch:
// Rekursiver Algo zum Bestimmen der Leaf-Node-Werte,
// die nach dem Minimax-Algo berechnet werden:
// Gespielt wird auf f, Züge werden bestimmt auf m,
// mm[tiefe] erhält die zu checkenden Züge,
// zuletzt wird f wieder auf den alten Stand gebracht
// --------------------------------------------------
function getopt(dran,tiefe)
{ if (tiefe==1) return getmax(dran); // ramschen
// gemischte Strategie: zu Beginn und Ende wird gewechselt:
else if ((count<6) || (count>(64-tiefe)) return getmax(dran);
else
{ // Werte und Zug initialisieren:
var i,j,wert=minimum,zug=-1,meinwert,seinwert,t;
// aktuellen Spielstand sichern, Zugliste erstellen:
for (i=0; i<f.length; i++) ff[tiefe][i]=f[i];
listenaufbau(dran);
// abgearbeitet wird mm[tiefe], da sich m ändert:
for (i=0; i<=m[0]; i++) mm[tiefe][i]=m[i];
if (mm[tiefe][0]>0) for (i=1; i<=mm[tiefe][0]; i++)
{ umdrehen(dran,mm[tiefe][i]);
// gegnerische Antwort bestimmen sowie deren
// Leaf-Node-Wert, der von getmax "heraufgereicht" wird:
gegner=(dran+1)%2;
seinwert=getopt(gegner,(tiefe-1));
seinwert=seinwert.split('p');
// des einen Freud, des anderen Leid:
meinwert=-seinwert[1];
if (meinwert>=wert) { zug=mm[tiefe][i]; wert=meinwert; }
// aktuellen Spielstand wiederherstellen
for (j=0; j<f.length; j++) f[j]=ff[tiefe][j];
}
return zug+'p'+wert;
}
}
Tiefe=3 spielt sich hiermit noch recht flüssig, bei Tiefe=4 dauert das Ganze zu lange, so dass es im Mittelteil der Partie Timeouts gibt (Ein Script verursachte...), schade eigentlich! Denn bei Tiefe 4 läuft erst nicht nur dieses Programm zu voller Schönheit auf! Denn bei Tiefe=3 ist der Computer zu sehr damit beschäftigt, die Strategie seines Gegners zu durchkreuzen, kann aber noch nicht weit genug sehen, um seine Vorteile zu erkennen. Die Spieletheoretiker nennen das: der Vorteil liegt jenseits seines Ereignishorizontes.
Deshalb wird zu Beginn den Spiels auf die Strategie "strategische Plätze um jeden Preis=ramscher" umgestiegen. Zum Ende hin würde sich "KlauWasteKanzz" empfehlen, aber "ramscher" bringt auch beste Ergebnisse.
Die Computerstrategie lässt sich bestimmt noch verbessern durch Feilen an der Wertematrix, an den Stationen, wo zwischen den einzelnen Strategien umgeschaltet wird, an der Beschleunigung der Funktionen für die Computerstrategie. Eventuell gibt es einen Geschwindigkeitsvorteil, wenn man statt mit 2dimensionalen Arrays wieder mit eindimensionalen Arrays arbeitet. Viellleicht kann man ja dann doch mal Stufe 4 spielen, die im Mittelteil nur max. eine halbe Minute mehr Zeit braucht, als der IE-Timeout zulässt. Das Umschalten der Computerstrategie auf "Ramscher" oder "KlauWasteKannz" muss dann natürlich angepasst werden.
Es gibt noch viel zu tun! ...
| zum Seitenanfang | ||
| zum Seitenende |